建築の部位・部材の稜線や隅は、平行、直角で構成されることが多い。この建築ならではの条件を使って、平面情報から奥行情報を推定することができる。
難しい説明
建築物の外壁や窓、内観写真なら壁、床、天井、開口部などは鉛直、水平に配置されることが多いです。部材どうしは、平行とか直角とかに配置されることが多いです。
1枚の写真(あるいはパース)から3次元情報を得るためには、失われた奥行情報を、建築物ならではの平行、直角を利用します。
なので、くにゃくにゃした建築物や斜めの部材でできた建築物の写真は、思い切って無視します。
それらを立体化するには、やっぱり2枚以上の写真が必要ですよね。簡単な説明をどうぞ。
さて、難しく説明すると、こういうことです。
- 写真から部材のエッジを抽出する。
- エッジを延長して、2つの消失点を求める。
- (平面図に視点を移して)2つの消失点を直径とする円弧と、写真の中心を通り写真に直交する直線との交点Eを求める。(これが写真を撮ったカメラの位置なのだ)
- 点Eと、2つの消失点を結ぶ2本の直線(直交している)が、部材のエッジに平行な直線である。つまり、写真の部材はこの2直線に平行である。
- あとは、点Eと写真上の点を結んだ先に、実世界の対応点があるので、それをつないでいけばよい。
はい、分かりません。書いている私も分かりません。
図で説明します。
今夜は、消失点を求めるところまで
たとえば、下のような内観写真があるとします。

これを画像処理にかけて、エッジを抽出します。

画像処理には、OpenCVのような便利な無料ツールがありますから、そういうのを使うといいでしょう。
(容赦ないですが、)ここでは理論を説明しているので、とりあえず、エッジが抽出できたとします。
さらに、エッジを数式で表しましょう。
ここに一つ山があります。プログラムを書く上で、ひとまとまりのエッジを取り出し、それを直線の式に変換する必要があるわけです。
(容赦ないですが、)ここでは理論を説明しているので、とりあえず、エッジの直線の式が得られたとします。
多数のエッジがあるので、数式も多数あると思います。
それらのうち、鉛直方向のものを排除しましょう。これは簡単ですね。
ax + by + z = 0 という式であれば、a/bの絶対値が大きいものを排除すればいいです。
y = ax + b という式でいえば、aの絶対値が大きいものを排除するということです。
これで、エッジの多くが水平線の直線を含むことになります。
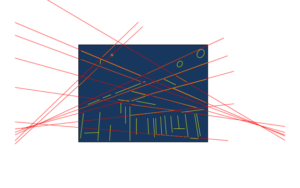
この残された直線は、およそ2つの点で交わることが期待できます。
統計的な処理をして、多くの直線との距離の合計が小さくなるような点を選びましょう。
(容赦ないですが、)ここでは理論を説明しているので、とりあえず、2つの点、すなわち消失点が得られたとします。
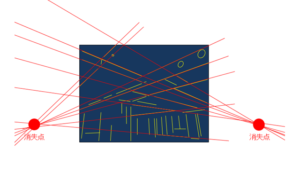
そうです。写真からエッジ抽出して、それらの直線を延長して、2つの交点を求めることで、透視図でいう消失点を求めることができるわけです。
途中で、はしょったところは?
理論の説明なので、ここでは具体的なプログラミング技法は説明しませんが、写真からエッジを取り出すのは、OpenCVなどの画像処理ライブラリを使えば難なくできます。
エッジ画像から、個々のエッジを取り出すのはちょっと面倒かもしれません。実際の写真からエッジを抽出すると、パラメータの選び方によっては、夥しい(おびただしい、と読みます)数の、ノイズのような短いエッジが得られることになるかもしれません。なので、ちょっと工夫が必要になるでしょう。
エッジから直線の式を求めるのは、程度によります。両端から直線の式を求めるのもよし、エッジを構成しているすべての点から最小二乗法で直線の式を求めるのもよし、計算時間と精度との綱引きで手法を決めましょう。
複数の直線の式から、2つの交点を求めるのは、やはり統計的な処理が必要になります。できれば、左右の消失点を求めるための直線をあらかじめ分離しておくのがいいと思います。例の写真であれば、画像の上半分に現れる直線のうち、傾きが正のものは左の消失点、傾きが負のものは右の消失点を求めるために使うとかですね。このあたりも、写真の撮り方とか、カメラのあおり具合とかにも影響を受けますから、いくつかの仮定で消失点を求め、その消失点から水平線を仮定してから、再度、水平線を境に上と下の領域で絞り込んだ直線で、あらためて正確な消失点を求める、なんて複数回の処理によって正確な消失点に近づけるなんて方法でもOK。
まだまだ先は長そうなので、今夜はこれまで。