ディープラーニングって、分かっちゃえば簡単だが、ひと言で言おうとすると、なかなかうまく言えない。
少しくらい不正確でもいいから、画像認識を1分で説明してみる。
ディープラーニングは分類をする
ディープラーニングは、画像を分類するものである。
それだけ。
入力した画像を、あらかじめ決めておいた数のカテゴリーのうち、どれに近いかを推定するだけです。
その、一つひとつのカテゴリーに「猫」とか「自動車」とか、分かりやすい名前をつけておけば、入力した画像は「猫」に近いとか、「自動車」に近いとか、言い当ててくれるわけです。
ディープラーニングは、ピクセルの濃さからカテゴリーを推定する
ディープラーニングは、結局のところ、一次方程式の計算を繰り返して、最終的に、1とか2とか、整数値を算出しています。算出された1とか2とかが、「猫」とか「自動車」に対応しています。
その一次方程式に入れる数値は、画像のピクセルの濃さです。

入力する自動車画像のピクセルの濃さ
画像のピクセルの濃さに、なんらかの係数を掛けて出した数値を、また係数を掛けて数値を出して、…

ほんとうは、こんなことを数回から数十回、繰り返しますが、ここでは早速、答えを計算します。
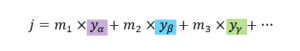
もし、jが1なら「猫」、2なら「自動車」と推定します。
ディープラーニングは係数を調整することで学習する
もしも、「自動車」の画像を入力したのに、答えが1と計算された(つまり「猫」と推定された)としたら、正しい答えに少しだけ近づくように、上の式の係数(a1, a2, a3, b1, b2, b3, c1, c2, c3, α1, α2, α3, β1, β2, β3, γ1, γ2, γ3, m1, m2, m3)を微調整します。
これを、膨大な量の画像を使って、何千回、何万回と繰り返し、微調整をひたすら繰り返すと、最後には、ほぼ正しい答えを出す方程式ができあがります。
これがディープラーニングが学習する仕組みです。
以上。
1分で読めましたか?
実は説明しなかった嘘
ところで、勘のいいひとなら、数式の説明がおかしいことに気づいたかもしれません。
「最初の式で出てきた数値を、つぎの式に入れてくということは、結局、ひとつの式にまとめられるんじゃないの?」
はい、説明を省きました。
ひとつの式にまとめられるということは、結局1回しか計算しないのと同じなので、複雑な分類はできません。
実は、式の値(xa, xb, xc, …)を次の計算で使うときは、そのままの値を使わずに、「ある値より小さければ0とみなす」ような処理がなされます。なので、ひとつの式にまとめられるわけではありません。
言い方を変えると、このような非線形な関数を間に挟むことで、複雑な分類が可能になるということです。
「畳み込み」「オートエンコーダー」をスパイスに
ディープラーニングを人に説明するときに、「畳み込み」という言葉を使えば、
「このひと、ディープラーニングを知っているな」
と思わせる効果があります。
畳み込みは、人間の視覚を模擬した仕組みで、画像のなかの近い領域については、係数を調整していきますが、離れた領域については無視する(係数を0にする)という処理方法です。
この畳み込みによって、人間の視覚になぞらえて高精度な分類ができるようになっています。
もうひとつ、素人には早すぎる情報ですが、近年のディープラーニングが成功した理由のひとつに、「オートエンコーダー」の発明があります。
実は、上の式の係数を微調整しようとしたとき、最後のほうの係数(m1, m2, m3, …)は調整しやすいのに対して、上流の係数(a1, a2, a3, …, b1, b2, b3, …, c1, c2, c3, …)は、微調整の微調整の微調整の…となって、難しくなるのです。
つまり、かつては、あまりディープにしたところで、繰り返す意味があまりなかったわけです。
オートエンコーダーは、その調整を上流まで、うまいこと反映させる技術でして、これによって、ディープになればなるほど、複雑な分類ができることになりました。